Innehåll

• Steg
• Tips

Den rationella funktionen har formen y = N (x) / D (x), där N och D är polynom. För att plotta en sådan funktion exakt behöver du goda kunskaper i algebra, inklusive differentialberäkningar. Tänk på följande exempel: y = (2x - 6x + 5)/(4x + 2).

Steg

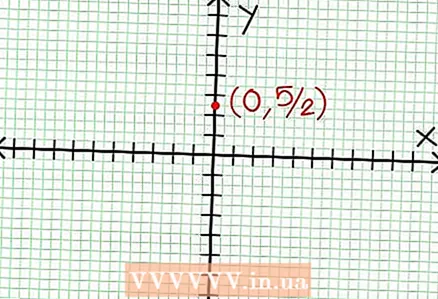1. 1 Hitta y-skärningen i grafen. För att göra detta, ersätt x = 0 i funktionen och få y = 5/2. Således har skärningspunkten för grafen med Y -axeln koordinater (0, 5/2).Placera denna punkt på koordinatplanet.
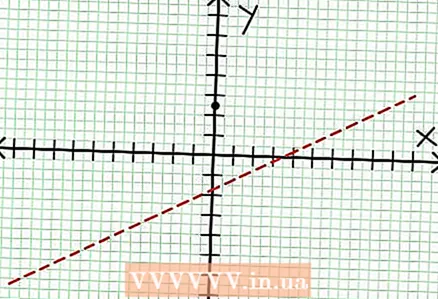2. 2 Hitta de horisontella asymptoterna. Dela täljaren med nämnaren (i en kolumn) för att bestämma beteendet för "y" med värden på "x" som tenderar till oändlighet. I vårt exempel kommer uppdelningen att vara y = (1/2)x - (7/4) + 17/(8x + 4). För stora positiva eller negativa värden på "x" 17 / (8x + 4) tenderar att nollas, och grafen närmar sig den raka linjen som ges av funktionen y = (1/2)x - (7/4). Plotta den här funktionen med den prickade linjen.
   • Om täljarens grad är mindre än nämnarens grad, kan du inte dela täljaren med nämnaren och asymptoten kommer att beskrivas av funktionen på = 0.
   • Om täljarens grad är lika med nämnarens grad, är asymptoten en horisontell linje lika med förhållandet mellan koefficienterna vid "x" i den högsta graden.
   • Om täljarens grad är 1 mer än nämnarens grad, är asymptoten en lutande rak linje, vars lutning är lika med förhållandet mellan koefficienterna vid "x" till den högsta graden.
   • Om täljarens grad är större än nämnarens grad med 2, 3, etc., då för stora värden |NS| menande på tenderar till oändlighet (positivt eller negativt) i form av en kvadratisk, kubisk eller annan grad av ett polynom. I det här fallet behöver du troligtvis inte skapa ett exakt diagram över funktionen som erhålls genom att dela täljaren med nämnaren.
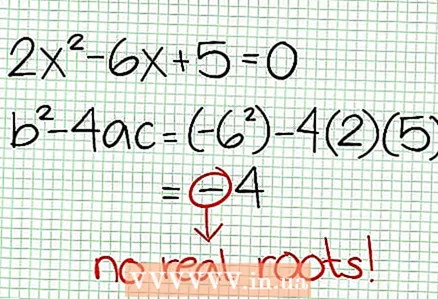3. 3 Hitta nollorna i funktionen. En rationell funktion har nollor när täljaren är noll, det vill säga N (NS) = 0. I vårt exempel, 2x - 6x + 5 = 0. Diskriminanten av denna kvadratiska ekvation: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Eftersom diskriminanten är negativ, då N (NS), och därmed F (NS) har inga riktiga rötter. Diagrammet för en rationell funktion skär inte X-axeln. Om funktionen har nollor (rötter), lägg dem sedan på koordinatplanet.
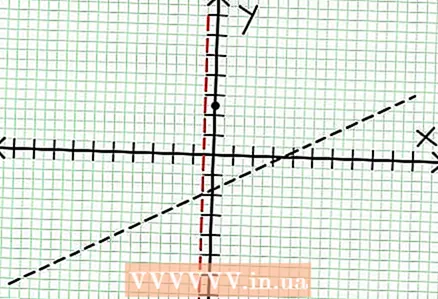4. 4 Hitta de vertikala asymptoterna. För att göra detta, ställ in nämnaren till noll. I vårt exempel, 4x + 2 = 0 och NS = -1/2. Plotta den vertikala asymptoten med den prickade linjen. Om för något värde NS N (NS) = 0 och D (NS) = 0, då finns den vertikala asymptoten antingen eller existerar inte (detta är ett sällsynt fall, men det är bättre att komma ihåg det).
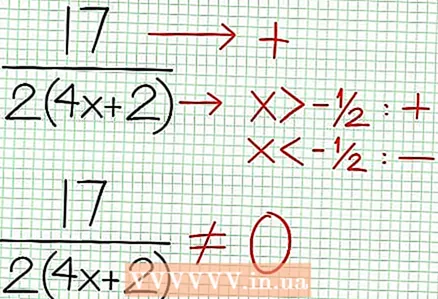5. 5 Titta på resten av täljaren dividerat med nämnaren. Är det positivt, negativt eller noll? I vårt exempel är resten 17, vilket är positivt. Nämnare 4x + 2 positiva till höger om den vertikala asymptoten och negativa till vänster om den. Detta innebär att grafen för den rationella funktionen för stora positiva värden NS närmar sig asymptoten ovanifrån och för stora negativa värden NS - underifrån. Sedan 17 / (8x + 4) är aldrig lika med noll, då kommer grafen för denna funktion aldrig att skär den raka linje som specificeras av funktionen på = (1/2)NS - (7/4).
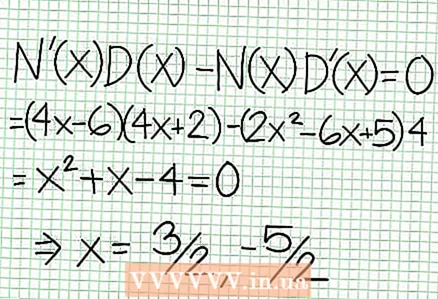6. 6 Hitta lokal extrema. Ett lokalt extremum finns för N '(x) D (x) - N (x) D ’(x) = 0. I vårt exempel är N ’(x) = 4x - 6 och D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. När du löser denna ekvation hittar du det x = 3/2 och x = -5/2. (Det här är inte helt korrekta värden, men de är lämpliga för vårt fall när superprecision inte behövs.)
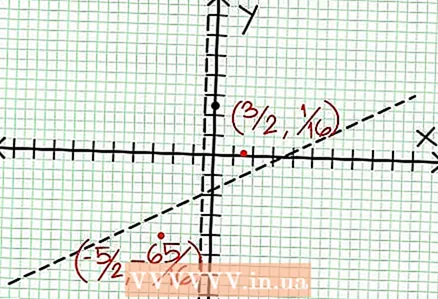7. 7 Hitta värdet på för varje lokal extremum. För att göra detta, ersätt värdena NS in i den ursprungliga rationella funktionen. I vårt exempel är f (3/2) = 1/16 och f (-5/2) = -65/16. Lägg åt sidan (3/2, 1/16) och (-5/2, -65/16) på koordinatplanet. Eftersom beräkningarna är baserade på ungefärliga värden (från föregående steg), är minimum och max som hittas inte heller helt korrekta (men förmodligen mycket nära de exakta värdena). (Punkten (3/2, 1/16) är mycket nära det lokala minimumet. Från steg 3 vet vi det på alltid positivt för NS> -1/2, och vi hittade ett litet värde (1/16); Därför är felvärdet extremt litet i det här fallet.)
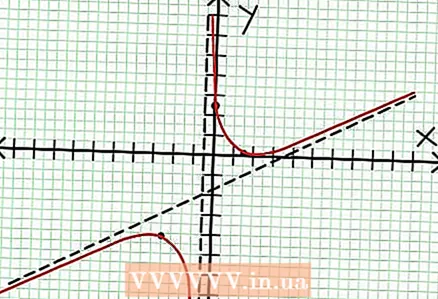8. 8 Anslut de väntande punkterna och förläng grafen smidigt till asymptoterna (glöm inte rätt riktning för grafen som närmar sig asymptoterna). Kom ihåg att diagrammet inte får korsa X-axeln (se steg 3). Diagrammet skär inte heller med de horisontella och vertikala asymptoterna (se steg 5). Ändra inte diagrammets riktning förutom vid de extrema punkter som hittades i föregående steg.

Tips

• Om du har följt stegen ovan i ordning behöver du inte beräkna de andra derivaten (eller liknande komplexa kvantiteter) för att testa din lösning.
• Om du inte behöver beräkna värdena på kvantiteter kan du ersätta att hitta lokal extrema genom att beräkna några ytterligare koordinatpar (NS, på) mellan varje par asymptoter. Om du inte bryr dig om hur den beskrivna metoden fungerar, bli inte förvånad över varför du inte kan hitta derivatet och lösa ekvationen N '(x) D (x) - N (x) D ’(x) = 0.
• I vissa fall måste du arbeta med högre ordningspolynom. Om du inte kan hitta den exakta lösningen med hjälp av faktorisering, formler, etc., uppskatta möjliga lösningar med hjälp av numeriska metoder som Newtons metod.
• I sällsynta fall delar täljaren och nämnaren en gemensam variabelfaktor. Enligt de beskrivna stegen leder detta till noll och en vertikal asymptot på samma plats. Detta är dock inte möjligt, och förklaringen är en av följande:
  • Noll i N (NS) har en högre mångfald än noll i D (NS). Diagram F (NS) tenderar till noll vid denna punkt, men definieras inte där. Ange detta genom att rita en cirkel runt punkten.
  • Noll i N (NS) och noll i D (NS) har samma mångfald. Diagrammet närmar sig någon icke-nollpunkt vid detta värde NSmen inte definierad däri. Ange detta genom att rita en cirkel runt punkten.
  • Noll i N (NS) har en lägre mångfald än noll i D (NS). Det finns en vertikal asymptot här.