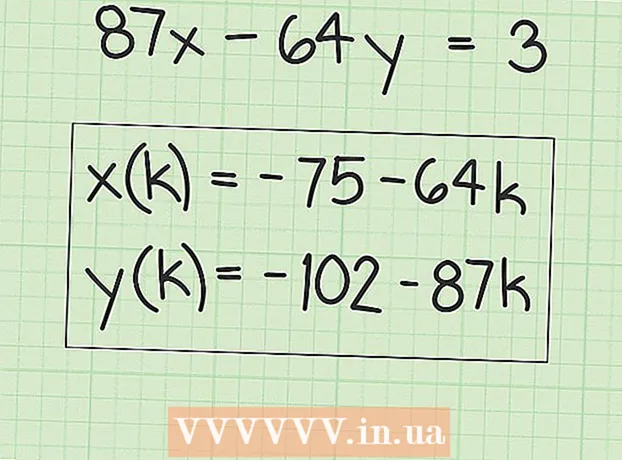
Innehåll

• Steg
• Del 1 av 4: Hur man skriver en ekvation
• Del 2 av 4: Hur man skriver Euklids algoritm
• Del 3 av 4: Hur man hittar en lösning med Euklids algoritm
• Del 4 av 4: Hitta oändliga andra lösningar

För att lösa en linjär Diophantine -ekvation måste du hitta värdena för variablerna "x" och "y", som är heltal. En heltalslösning är mer komplex än vanligt och kräver en specifik uppsättning åtgärder. Först måste du beräkna den största gemensamma divisorn (GCD) för koefficienterna och sedan hitta en lösning. När du har hittat en heltalslösning till en linjär ekvation kan du använda ett enkelt mönster för att hitta ett oändligt antal andra lösningar.

Steg

Del 1 av 4: Hur man skriver en ekvation

1. 1 Skriv ner ekvationen i standardform. En linjär ekvation är en ekvation där variablernas exponenter inte överstiger 1. För att lösa en sådan linjär ekvation, skriv den först i standardform. Standardformen för en linjär ekvation ser ut så här: ${ displaystyle Ax + By = C}$, var ${ displaystyle A, B}$ och ${ displaystyle C}$ - heltal.
   • Om ekvationen ges i en annan form, ta den till standardform med hjälp av grundläggande algebraiska operationer. Till exempel med tanke på ekvationen ${ displaystyle 23x + 4y -7x = -3y + 15}$... Ge liknande termer och skriv ekvationen så här: ${ displaystyle 16x + 7y = 15}$.
2. 2 Förenkla ekvationen (om möjligt). När du skriver ekvationen i standardform, titta på koefficienterna ${ displaystyle A, B}$ och ${ displaystyle C}$... Om dessa odds har en GCD, dela alla tre oddsen med det. Lösningen på en sådan förenklad ekvation kommer också att vara lösningen på den ursprungliga ekvationen.
   • Till exempel, om alla tre koefficienterna är jämna, dela dem med minst 2. Till exempel:
     • ${ displaystyle 42x + 36y = 48}$ (alla medlemmar är delbara med 2)
     • ${ displaystyle 21x + 18y = 24}$ (nu är alla medlemmar delbara med 3)
     • ${ displaystyle 7x + 6y = 8}$ (denna ekvation kan inte längre förenklas)
3. 3 Kontrollera om ekvationen kan lösas. I vissa fall kan du omedelbart konstatera att ekvationen inte har några lösningar. Om koefficienten "C" inte är delbar med GCD för koefficienterna "A" och "B" har ekvationen inga lösningar.
   • Till exempel om båda koefficienterna ${ displaystyle A}$ och ${ displaystyle B}$ är jämna, då är koefficienten ${ displaystyle C}$ måste vara jämn. Men om ${ displaystyle C}$ udda, då finns det ingen lösning.
     • Ekvationen ${ displaystyle 2x + 4y = 21}$ inga heltalslösningar.
     • Ekvationen ${ displaystyle 5x + 10y = 17}$ det finns inga heltalslösningar eftersom ekvatorns vänstra sida är delbar med 5 och höger sida inte.

Del 2 av 4: Hur man skriver Euklids algoritm

1. 1 Förstå Euclids algoritm. Det är en serie upprepade divisioner där den föregående återstoden används som nästa delare. Den sista divisorn som delar numren integrerat är den största gemensamma divisorn (GCD) av de två talen.
   • Låt oss till exempel hitta GCD för siffrorna 272 och 36 med hjälp av Euclids algoritm:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Dela det större numret (272) med det mindre (36) och var uppmärksam på resten (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - dela föregående delare (36) med föregående återstod (20). Notera den nya resten (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - dela föregående delare (20) med föregående återstod (16). Notera den nya resten (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Dela föregående delare (16) med föregående återstod (4). Eftersom resten är 0 kan vi säga att 4 är GCD för de två ursprungliga talen 272 och 36.
2. 2 Tillämpa Euclids algoritm på koefficienterna "A" och "B". När du skriver den linjära ekvationen i standardform, bestäm koefficienterna "A" och "B" och applicera sedan Euklids algoritm för att hitta GCD. Till exempel, ges en linjär ekvation ${ displaystyle 87x-64y = 3}$.
   • Här är Euklids algoritm för koefficienter A = 87 och B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Hitta den största gemensamma faktorn (GCD). Eftersom den sista divisorn var 1 är GCD 87 och 64 1. 87 och 64 är alltså primtal i förhållande till varandra.
4. 4 Analysera resultatet. När du hittar gcd -koefficienterna ${ displaystyle A}$ och ${ displaystyle B}$, jämför det med koefficienten ${ displaystyle C}$ den ursprungliga ekvationen. Om ${ displaystyle C}$ delbart med gcd ${ displaystyle A}$ och ${ displaystyle B}$, ekvationen har en heltalslösning; annars har ekvationen inga lösningar.
   • Till exempel ekvationen ${ displaystyle 87x-64y = 3}$ kan lösas eftersom 3 är delbart med 1 (gcd = 1).
   • Anta till exempel GCD = 5. 3 är inte jämnt delbart med 5, så denna ekvation har inga heltalslösningar.
   • Som visas nedan, om en ekvation har en heltalslösning, har den också ett oändligt antal andra heltalslösningar.

Del 3 av 4: Hur man hittar en lösning med Euklids algoritm

1. 1 Nummerera stegen för att beräkna GCD. För att hitta lösningen på en linjär ekvation måste du använda den euklidiska algoritmen som grund för substitutions- och förenklingsprocessen.
   • Börja med att numrera stegen för att beräkna GCD. Beräkningsprocessen ser ut så här:
     • ${ displaystyle { text {Steg 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Steg 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Steg 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Steg 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Steg 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Steg 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Steg 7}}: 2 = (2 * 1) +0}$
2. 2 Var uppmärksam på det sista steget, där det finns en återstod. Skriv om ekvationen för detta steg för att isolera resten.
   • I vårt exempel är det sista steget med resten steg 6. Resten är 1. Skriv om ekvationen i steg 6 enligt följande:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Isolera resten av föregående steg. Denna process är ett steg-för-steg "gå upp". Varje gång kommer du att isolera resten i ekvationen i föregående steg.
   • Isolera resten av ekvationen i steg 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ eller ${ displaystyle 2 = 5-3}$
4. 4 Ersätt och förenkla. Lägg märke till att ekvationen i steg 6 innehåller siffran 2, och i ekvationen i steg 5 är siffran 2 isolerad. Så istället för “2” i ekvationen i steg 6, ersätt uttrycket i steg 5:
   • ${ displaystyle 1 = 3-2}$ (ekvation i steg 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (istället för 2 ersattes ett uttryck)
   • ${ displaystyle 1 = 3-5 + 3}$ (öppna parenteser)
   • ${ displaystyle 1 = 2 (3) -5}$ (förenklat)
5. 5 Upprepa substitutions- och förenklingsprocessen. Upprepa den beskrivna processen, gå igenom den euklidiska algoritmen i omvänd ordning. Varje gång kommer du att skriva om ekvationen från föregående steg och ansluta den till den sista ekvationen du får.
   • Det sista steget vi tittade på var steg 5. Så gå till steg 4 och isolera resten i ekvationen för det steget:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Ersätt detta uttryck med "3" i den sista ekvationen:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Fortsätt med substitutions- och förenklingsprocessen. Denna process kommer att upprepas tills du når det första steget i den euklidiska algoritmen. Målet med processen är att skriva ekvationen med koefficienterna 87 och 64 i den ursprungliga ekvationen som ska lösas. I vårt exempel:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (ersatte uttrycket från steg 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (ersatte uttrycket från steg 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (ersatte uttrycket från steg 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Skriv om den resulterande ekvationen i enlighet med de ursprungliga koefficienterna. När du återgår till det första steget i den euklidiska algoritmen ser du att den resulterande ekvationen innehåller två koefficienter för den ursprungliga ekvationen. Skriv om ekvationen så att ordningen på termerna matchar koefficienterna för den ursprungliga ekvationen.
   • I vårt exempel, den ursprungliga ekvationen ${ displaystyle 87x-64y = 3}$... Skriv därför om den resulterande ekvationen så att koefficienterna anpassas.Var särskilt uppmärksam på koefficienten "64". I den ursprungliga ekvationen är denna koefficient negativ, och i den euklidiska algoritmen är den positiv. Därför måste faktorn 34 göras negativ. Den slutliga ekvationen kommer att skrivas så här:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Använd lämplig multiplikator för att hitta en lösning. Observera att i vårt exempel är GCD = 1, så den slutliga ekvationen är 1. Men den ursprungliga ekvationen (87x-64y) är 3. Därför måste alla termer i den slutliga ekvationen multipliceras med 3 för att få lösningen:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Skriv ner heltalslösningen till ekvationen. Siffrorna som multipliceras med koefficienterna för den ursprungliga ekvationen är lösningarna på den ekvationen.
   • I vårt exempel skriver du lösningen som ett par koordinater: ${ displaystyle (x, y) = ( - 75, -102)}$.

Del 4 av 4: Hitta oändliga andra lösningar

1. 1 Förstå att det finns ett oändligt antal lösningar. Om en linjär ekvation har en heltalslösning måste den ha oändligt många heltalslösningar. Här är ett snabbt bevis (i algebraisk form):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (om du lägger till "B" till "x" och subtraherar "A" från "y", ändras inte värdet på den ursprungliga ekvationen)
2. 2 Anteckna de ursprungliga x- och y -värdena. Mallen för att beräkna nästa (oändliga) lösningar börjar med den enda lösningen du redan har hittat.
   • I vårt exempel är lösningen ett par koordinater ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Lägg till "B" -faktorn till "x" -värdet. Gör detta för att hitta det nya x -värdet.
   • I vårt exempel x = -75 och B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Således är det nya värdet "x": x = -139.
4. 4 Subtrahera "A" -faktorn från "y" -värdet. Så att värdet på den ursprungliga ekvationen inte ändras, när du lägger till ett tal till "x", måste du subtrahera ett annat tal från "y".
   • I vårt exempel y = -102 och A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Således är det nya värdet för "y": y = -189.
   • Det nya paret koordinater kommer att skrivas så här: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Kontrollera lösningen. För att verifiera att det nya koordinatparet är en lösning på den ursprungliga ekvationen, anslut värdena till ekvationen.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Eftersom jämställdheten är uppfylld är beslutet korrekt.
6. 6 Skriv ner uttryck för att hitta många lösningar. "X" -värdena kommer att motsvara den ursprungliga lösningen plus eventuell multipel av "B" -faktorn. Detta kan skrivas som följande uttryck:
   • x (k) = x + k (B), där "x (k)" är mängden "x" -värden och "x" är det ursprungliga (första) värdet för "x" som du hittade.
     • I vårt exempel:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), där y (k) är mängden y-värden och y är det ursprungliga (första) y-värdet som du hittade.
     • I vårt exempel:
     • ${ displaystyle y (k) = - 102-87k}$