Hur man beräknar momentan hastighet: 11 steg (med foto) - Tips

Video: Instantaneous speed and velocity | One-dimensional motion | Physics | Khan Academy

Innehåll

Steg
Råd

Hastighet definieras som ett objekts hastighet i en given riktning. För att hitta hastighet använder vi i många fall ekvationen v = s / t, där v är hastigheten, s är det totala avståndet för objektets förskjutning från dess ursprungliga läge, och t är den tid det tar för objektet att färdas. gå hela vägen. Men i teorin är denna formel endast för hastighet medium av saker på vägen. Genom att beräkna objektets hastighet vid varje given tidpunkt längs avståndet. Det är Transporttid och definieras av ekvationen v = (ds) / (dt), eller med andra ord, det är derivatet av ekvationen för medelhastigheten.

Steg

Del 1 av 3: Beräkna momentan hastighet

Börja med en ekvation för beräkning av hastighet efter förskjutningsavstånd. För att hitta den momentana hastigheten måste vi först ha en ekvation som anger objektets position (i termer av förskjutning) vid varje given tidpunkt. Det betyder att ekvationen bara måste ha en variabel S på ena sidan och vänd t På andra sidan (inte nödvändigtvis bara en variabel), så här:
s = -1,5t + 10t + 4
- I denna ekvation är variablerna:
  s = förskjutning. Avståndet objektet rörde sig från dess ursprungliga position. Till exempel, om ett objekt kan gå 10 meter framåt och 7 meter bakåt, är dess totala färdsträcka 10 - 7 = 3 meter (inte 10 + 7 = 17m).
  t = tid. Denna variabel är enkel utan förklaring, vanligtvis mätt i sekunder.
Ta derivatet av ekvationen. Derivat av ekvationen är en annan ekvation som visar avståndets lutning vid en viss tidpunkt. För att hitta ekvationens derivat med förskjutningsavstånd, ta funktionens differential enligt följande allmänna regel för att beräkna derivatet: Om y = a * x, Derivat = a * n * x. Detta gäller för alla termer på "t" -sidan av ekvationen.
- Med andra ord, börja få differentialen från vänster till höger på "t" -sidan av ekvationen. När du stöter på variabeln "t" subtraherar du exponenten med 1 och multiplicerar termen med den ursprungliga exponenten. Alla konstanta termer (termer utan "t") försvinner eftersom de multipliceras med 0. Processen är faktiskt inte så svår som du kanske tror - låt oss ta ekvationen i steget ovan som ett exempel:
  s = -1,5t + 10t + 4
  (2) -1,5t + (1) 10t + (0) 4t
  -3t + 10t
  -3t + 10
Ersätt "s" med "ds / dt". För att visa att den nya ekvationen är derivatet av den ursprungliga kvadraten ersätter vi "s" med symbolen "ds / dt". I teorin är denna notation "derivat av s i termer av t". Ett enklare sätt att förstå denna notation, ds / dt är lutningen för vilken punkt som helst i den ursprungliga ekvationen. Till exempel, för att hitta lutningen på avståndet som beskrivs av ekvationen s = -1,5t + 10t + 4 vid tiden t = 5, ersätter vi "5" för t i derivatan av ekvationen.
- I exemplet ovan ser derivatet av ekvationen ut så här:
  ds / dt = -3t + 10
Ersätt ett värde för t i den nya ekvationen för att hitta momentan hastighet. Nu när vi har den härledda ekvationen är det mycket enkelt att hitta den momentana hastigheten vid varje givet ögonblick. Allt du behöver göra är att välja ett t-värde och ersätta det med derivatekvationen. Om vi till exempel vill hitta den momentana hastigheten vid t = 5, behöver vi bara ersätta "5" för t i derivatekvationen ds / dt = -3t + 10. Vi löser ekvationen så här:
ds / dt = -3t + 10
ds / dt = -3 (5) + 10
ds / dt = -15 + 10 = -5 meter / sekund
- Observera att vi använder enheten "meter / sekund" ovan.Eftersom vi löser problemet med förskjutning i meter och tid i sekunder, och hastighet är förskjutning i tid, är den här enheten lämplig.
annons

Del 2 av 3: Uppskatta momentan hastighet grafiskt

Grafer objektets rörelseavstånd över tiden. I avsnittet ovan sa vi att derivatet också är en formel som gör att vi kan hitta lutningen vid vilken punkt som helst i ekvationen från derivatet. Faktum är att om du visar objektets rörliga avstånd i en graf, Lutningen på diagrammet vid någon punkt är objektets momentana hastighet vid den punkten.
- För att rita rörelseavstånd, använd x-axeln för tid och y-axeln för förskjutning. Du bestämmer sedan ett antal punkter genom att ansluta värdena för t i rörelseekvationen, resultatet är s-värden och du prickar punkterna t, s (x, y) i diagrammet.
- Observera att diagrammet kan sträcka sig under x-axeln. Om linjen som visar objektets rörelse går ner på x-axeln betyder det att objektet rör sig bakåt från sitt ursprungliga läge. I allmänhet sträcker sig diagrammet inte bakom y-axeln - vi mäter vanligtvis inte hastigheten på objekt som rör sig tillbaka i tiden!
Välj en punkt P och en punkt Q som ligger nära punkten P i diagrammet. För att hitta lutningen på diagrammet vid punkten P använder vi tekniken för "gränssökning". Att hitta en gräns innebär att ta två punkter (P och Q (en punkt nära P)) på kurvan och hitta lutningen på linjen som förbinder dessa två punkter, och upprepa denna process när avståndet mellan P och Q förkortas. gradvis.
- Antag att förskjutningsavståndet har punkter (1; 3) och (4; 7). I det här fallet, om vi vill hitta lutningen vid (1; 3) kan vi ställa in (1; 3) = P och (4; 7) = Q.
Hitta lutningen mellan P och Q. Lutningen mellan P och Q är skillnaden mellan y-värdena för P och Q över skillnaden mellan x-värdena för P och Q. Med andra ord, H = (y_F - y_P) / (x_F - x_P), där H är lutningen mellan två punkter. I detta exempel är lutningen mellan P och Q:
H = (y_F - y_P) / (x_F - x_P)
H = (7 - 3) / (4 - 1)
H = (4) / (3) = 1,33
Upprepa flera gånger genom att flytta Q närmare P. Målet är att begränsa avståndet mellan P och Q tills de når en enda punkt. Ju mindre avståndet mellan P och Q är, desto närmare kommer det oändligt lilla segmentets lutning till lutningen vid punkt P. Upprepa några gånger för vårt exempel på ekvation med hjälp av punkter (2; 4 , 8), (1.5; 3.95) och (1.25; 3.49) ger Q och de initiala koordinaterna för P är (1; 3):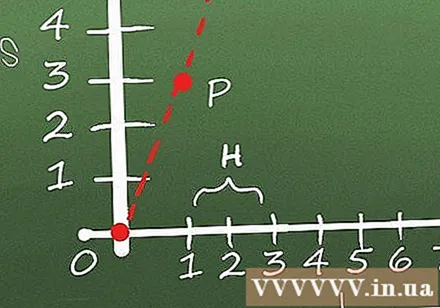
Q = (2; 4,8): H = (4,8 - 3) / (2 - 1)
H = (1,8) / (1) = 1,8

Q = (1,5; 3,95): H = (3,95 - 3) / (1,5 - 1)
H = (0,95) / (0,5) = 1,9

Q = (1,25; 3,49): H = (3,49 - 3) / (1,25 - 1)
H = (0,49) / (0,25) = 1,96
Uppskattar lutningen för det extremt lilla segmentet i grafkurvan. När Q kommer närmare och närmare P kommer H gradvis närmare lutningen vid P. Slutligen, vid en mycket liten linje, kommer H att vara lutningen vid P. Eftersom vi inte kan mäta eller beräkna Längden på en linje är extremt liten, så uppskatta endast lutningen vid P när den syns tydligt från de punkter vi beräknar.
- I exemplet ovan, när vi flyttar H närmare P, har vi värdena för H på 1,8; 1,9 och 1,96. Eftersom dessa siffror närmar sig 2 kan vi säga 2 är det ungefärliga värdet för lutningen vid P.
- Kom ihåg att lutningen vid någon punkt i diagrammet är derivatet av grafekvationen vid den punkten. Eftersom grafen visar ett objekts förskjutning över tiden, som vi såg i föregående avsnitt, är dess momentana hastighet vid vilken punkt som helst härledd till objektets förskjutningsavstånd vid problempunkten. Tillgång, kan vi säga 2 meter / sek är en ungefärlig uppskattning av den momentana hastigheten när t = 1.
annons

Del 3 av 3: Provproblem

Hitta den momentana hastigheten när t = 1 med förskjutningsekvationen s = 5t - 3t + 2t + 9. Liksom exemplet i det första avsnittet, men detta är en kubik istället för kvadratisk, så vi kan lösa problemet på samma sätt.
- Ta först derivatan av ekvationen:
  s = 5t - 3t + 2t + 9
  s = (3) 5t - (2) 3t + (1) 2t
  15t - 6t + 2t - 6t + 2
- Sedan ersätter vi värdet på t (4) i:
  s = 15t - 6t + 2
  15(4) - 6(4) + 2
  15(16) - 6(4) + 2
  240 - 24 + 2 = 22 meter per sekund
Använd metoden för grafuppskattning för att hitta den momentana hastigheten vid (1; 3) för förskjutningsekvationen s = 4t - t. För detta problem använder vi koordinater (1; 3) som punkt P, men vi måste hitta andra Q-punkter som ligger nära den. Allt vi behöver göra är att hitta H-värdena och dra upp det uppskattade värdet.
- Först hittar vi Q-punkter när t = 2; 1,5; 1.1 och 1.01.
  s = 4t - t
  
  t = 2: s = 4 (2) - (2)
  4 (4) - 2 = 16 - 2 = 14, så Q = (2; 14)
  
  t = 1,5: s = 4 (1,5) - (1,5)
  4 (2,25) - 1,5 = 9 - 1,5 = 7,5, så Q = (1,5; 7,5)
  
  t = 1,1: s = 4 (1.1) - (1.1)
  4 (1,21) - 1,1 = 4,84 - 1,1 = 3,74, så Q = (1,1; 3,74)
  
  t = 1,01: s = 4 (1,01) - (1,01)
  4 (10201) - 1,01 = 4,0804 - 1,01 = 3,0704, så det är det Q = (1,01; 3,0704)
- Därefter får vi H-värden:
  Q = (2; 14): H = (14 - 3) / (2 - 1)
  H = (11) / (1) = 11
  
  Q = (1,5; 7,5): H = (7,5 - 3) / (1,5 - 1)
  H = (4,5) / (0,5) = 9
  
  Q = (1,1; 3,74): H = (3,74 - 3) / (1,1 - 1)
  H = (0,74) / (0,1) = 7,3
  
  Q = (1,01; 3,0704): H = (3,0704 - 3) / (1,01 - 1)
  H = (0,0704) / (0,01) = 7,04
- Eftersom H-värden verkar vara närmare 7 kan vi säga det 7 meter per sekund är den ungefärliga uppskattningen av den momentana hastigheten vid koordinaten (1; 3).
annons

Råd

För att hitta acceleration (förändring av hastighet över tid), använd metoden i del ett för att få derivatet av förskjutningsekvationen. Ta sedan derivatet igen för den derivat ekvation du just hittade. Som ett resultat har du en ekvation för accelerationen vid en viss tidpunkt - allt du behöver göra är att ansluta tiden.
Ekvationen som visar förhållandet mellan Y (förskjutningsavstånd) och X (tid) kan vara väldigt enkel, som Y = 6x + 3. I detta fall är lutningen konstant och det är inte nödvändigt att ta derivatet för beräkning av lutningen, det vill säga, det följer den grundläggande ekvationsformen Y = mx + b för en linjär graf, dvs lutningen är lika med 6.
Förskjutningsavståndet är detsamma som avståndet men har en riktning, så det är en vektormängd och hastighet är en skalär kvantitet. Reseavstånd kan vara negativa, medan avstånd bara kan vara positiva.