Innehåll

• Steg
• Råd

Till skillnad från en rak linje förändras lutningskoefficienten (lutning) ständigt när den rör sig längs kurvan. Calculus ger idén att varje punkt i diagrammet kan uttryckas som en vinkelkoefficient eller "ögonblicklig förändringshastighet". Tangentlinjen vid en punkt är en linje som har samma vinkelkoefficient och passerar genom samma punkt. För att hitta en tangentlinjeekvation måste du veta hur man härleder den ursprungliga ekvationen.

Steg

Metod 1 av 2: Hitta ekvationen för tangentlinjen

1. 

   Graffunktioner och tangentlinjer (detta steg är valfritt, men rekommenderas). Diagrammet hjälper dig lättare att förstå problemet och kontrollera om svaret är rimligt eller inte. Rita funktionsdiagram på rasterpapper, använd den vetenskapliga räknaren med graffunktion för referens om det behövs. Rita en tangentlinje genom en viss punkt (Kom ihåg att tangentlinjen passerar genom den punkten och har samma lutning som diagrammet där).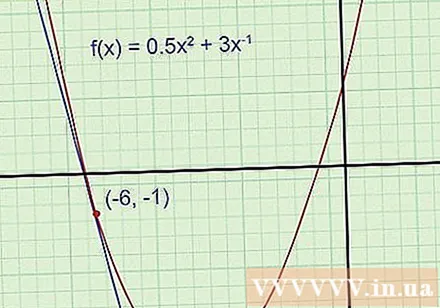
   • Exempel 1: Parabolisk ritning. Rita en tangentlinje genom punkten (-6, -1).
     Även om du inte känner till tangentekvationen kan du fortfarande se att dess lutning är negativ och skärningspunkten är negativ (långt under parabolspetsen med ordinaten -5,5). Om det slutliga svaret som hittades inte överensstämmer med dessa uppgifter måste det finnas ett fel i din beräkning och du måste kontrollera igen.

2. 

   
   
   Få det första derivatet för att hitta ekvationen backe av tangentlinjen. Med funktionen f (x) representerar det första derivatet f '(x) ekvationen för tangentlinjens lutning vid vilken punkt som helst på f (x). Det finns många sätt att ta derivat. Här är ett enkelt exempel med kraftregeln:
   • Exempel 1 (forts.): Grafen ges av en funktion.
     Återkallar kraftregeln när du tar derivat:.
     Det första derivatet av funktionen = f '(x) = (2) (0,5) x + 3 - 0.
     f '(x) = x + 3. Genom att ersätta x med valfritt värde a kommer ekvationen att ge oss lutningen för tangentfunktionen f (x) vid punkten x = a.

3. 

   
   
   Ange x-värdet för den aktuella punkten. Läs problemet för att hitta koordinaterna för punkten för att hitta tangentlinjen. Ange koordinaten för denna punkt i f '(x). Det erhållna resultatet är lutningen för tangentlinjen vid ovanstående punkt.
   • Exempel 1 (forts.): Poängen som nämns i artikeln är (-6, -1). Med diagonal -6 spänning till f '(x):
     f '(- 6) = -6 + 3 = -3
     Tangentlinjens lutning är -3.

4. 

   
   
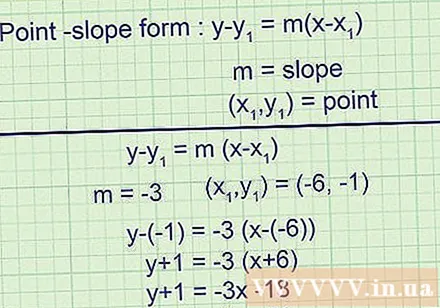
   Skriv en ekvation för en tangentlinje med formen av en rak linje som vet vinkelkoefficienten och en punkt på den. Denna linjära ekvation skrivs som. Inuti, m är lutningen och är en punkt på tangentlinjen. Du har nu all information du behöver för att skriva en tangentekvation i denna form.
   • Exempel 1 (forts.):
     Tangentlinjens lutning är -3, så:
     Tangentlinjen passerar genom punkten (-6, -1), så den slutliga ekvationen är:
     Kort sagt kan vi:
     

5. 

   Grafisk bekräftelse. Om du har en grafkalkylator, plotta originalfunktionen och tangentlinjen för att kontrollera om svaret är korrekt. Om du gör beräkningar på papper, använd diagram ritade tidigare för att se till att det inte finns några uppenbara fel i ditt svar.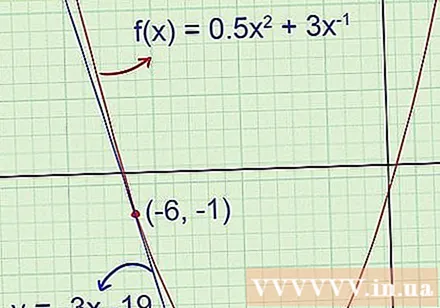
   • Exempel 1 (forts.): Den ursprungliga ritningen visar att tangentlinjen har negativa vinkelkoefficienter och förskjutningen är långt under -5,5. Tangentekvationen som just hittats är y = -3x -19, vilket betyder att -3 är lutningen på vinkeln och -19 är ordinaten.

6. 

   Försök att lösa ett svårare problem. Vi går igenom alla stegen ovan igen.Vid denna tidpunkt är målet att hitta tangentlinjen på x = 2: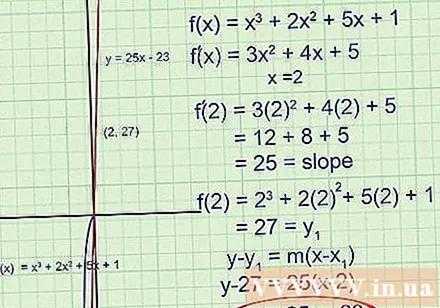
   • Hitta det första derivatet med kraftregeln :. Denna funktion ger oss tangentens lutning.
   • För x = 2, hitta. Detta är lutningen vid x = 2.
   • Observera att den här gången har vi ingen punkt och bara x-koordinaten. För att hitta y-koordinaten, ersätt x = 2 i originalfunktionen :. Poängen är (2.27).
   • Skriv en ekvation för en tangentlinje som går genom en punkt och har koefficienten för vinkeln bestämd:
     
     Sänk vid behov till y = 25x - 23.
   annons

Metod 2 av 2: Lös relaterade problem

1. 

   Hitta det extrema i diagrammet. De är de punkter där grafen närmar sig ett lokalt maximum (en punkt högre än närliggande punkter på båda sidor) eller ett lokalt minimum (lägre än närliggande punkter på båda sidor). Tangentlinjen har alltid en nollkoefficient vid dessa punkter (en horisontell linje). Vinkelkoefficienten är emellertid inte tillräcklig för att dra slutsatsen att det är den extrema punkten. Så här hittar du dem: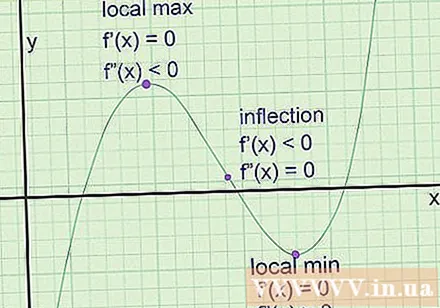
   • Ta det första derivatet av funktionen för att få f '(x), lutningen för lutningen för tangentlinjen.
   • Lös ekvationen f '(x) = 0 för att hitta extrempunkten potential.
   • Tar vi det kvadratiska derivatet för att få f '(x), berättar ekvationen förändringshastigheten för tangentlinjens lutning.
   • Ändra koordinaten vid varje potentiell extrem a in i f '' (x). Om f '(a) är positivt har vi ett lokalt minimum vid a. Om f '(a) är negativ, har vi en lokal maximal punkt. Om f '(a) är 0 blir det inte extremt, det är en böjningspunkt.
   • Om max eller min nås kl a, hitta f (a) för att bestämma korsningen.

2. 

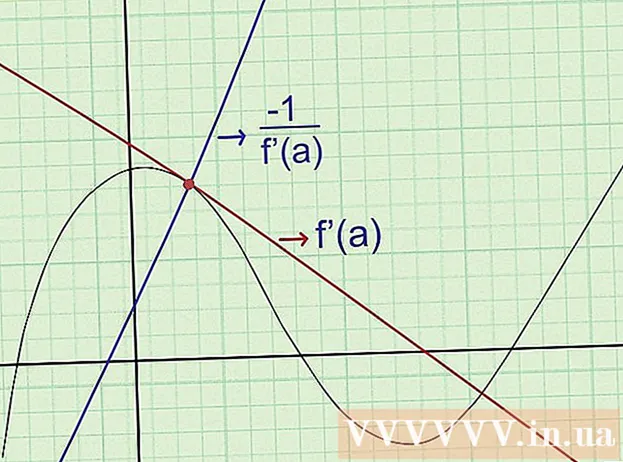
   Hitta ekvationerna för det normala. Den "normala" linjen i en kurva vid en given punkt a passerar genom den punkten och är vinkelrät mot tangentlinjen. För att hitta ekvationen för det normala, använd följande: (normalens lutning) (normalens lutning) = -1 när de passerar samma punkt i diagrammet. Specifikt: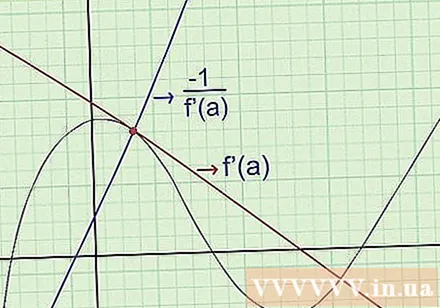
   • Hitta f '(x), tangentlinjens lutning.
   • Om vi ​​vid en given punkt har x = a: hitta f '(a) för att bestämma lutningen vid den punkten.
   • Beräkna för att hitta koefficienten för det normala.
   • Skriv ekvationen för vinkelrätt mot att känna koefficienterna för vinkeln och en punkt den passerar igenom.
   annons

Råd

• Om nödvändigt, skriv om originalekvationen i standardform: f (x) = ... eller y = ...