Innehåll

• Steg
• Del 1 av 3: Enkeltest
• Del 2 av 3: Hur enkelhetstester fungerar
• Del 3 av 3: Användning av den kinesiska restsatsen
• Tips
• Vad behöver du

Primtal är tal som endast är delbara med sig själva och med 1. Alla andra nummer kallas sammansatta tal. Det finns många sätt att avgöra om ett tal är primtal, och de har alla sina egna fördelar och nackdelar. Å ena sidan är några av metoderna mycket exakta, men de är ganska komplexa om du har att göra med stora siffror. Å andra sidan finns det mycket snabbare sätt, men de kan leda till felaktiga resultat. Valet av lämplig metod beror på hur stora siffror du arbetar med.

Steg

Del 1 av 3: Enkeltest

Notera: i alla formler n betecknar numret som ska kontrolleras.

1. 1 Uppräkning av delare. Det räcker med att dela n till alla primtal från 2 till det avrundade värdet (${ displaystyle { sqrt {n}}}$).
2. 2 Fermats lilla sats. Varning: ibland kan testet felaktigt identifiera sammansatta tal som primtal, även för alla värden på a.
   • Låt oss välja ett heltal aså att 2 ≤ a ≤ n - 1.
   • Om a (mod n) = a (mod n) är siffran förmodligen primtal. Om jämlikheten inte uppfylls är siffran n sammansatt.
   • Kontrollera given jämlikhet för flera värden aför att öka sannolikheten för att antalet som testas verkligen är utmärkt.
3. 3 Miller-Rabin test. Varning: ibland, men sällan, för flera värden på a, kommer testet felaktigt att identifiera sammansatta tal som primtal.
   • Hitta mängderna s och d så att ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Välj ett heltal a i intervallet 2 ≤ a ≤ n - 1.
   • Om a = +1 (mod n) eller -1 (mod n), är n förmodligen primtal. Gå i så fall till testresultatet. Om jämlikheten inte håller, gå till nästa steg.
   • Kvittera ditt svar (${ displaystyle a ^ {2d}}$). Om du får -1 (mod n), är n förmodligen ett primtal. Gå i så fall till testresultatet. Om jämlikheten misslyckas, upprepa (${ displaystyle a ^ {4d}}$ och så vidare) tills ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • Om vid något steg efter kvadrering av ett annat nummer än ${ displaystyle pm 1}$ (mod n), du har +1 (mod n), så n är ett sammansatt tal. Om ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), då är n inte primtal.
   • Testresultat: om n klarar testet, upprepa det för andra värden aatt öka förtroendet.

Del 2 av 3: Hur enkelhetstester fungerar

1. 1 Uppräkning av delare. Per definition, antalet n är enkelt bara om det inte är delbart med 2 och andra heltal utom 1 och sig själv. Ovanstående formel låter dig ta bort onödiga steg och spara tid: till exempel, efter att ha kontrollerat om ett tal är delbart med 3, behöver du inte kontrollera om det är delbart med 9.
   • Golvfunktionen (x) avrundar x till närmaste heltal mindre än eller lika med x.
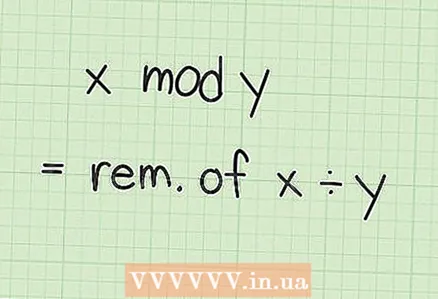2. 2 Lär dig om modulär aritmetik. Operationen "x mod y" (mod är en förkortning av det latinska ordet "modulo", det vill säga "modul") betyder "dela x med y och hitta resten." Med andra ord, i modulär aritmetik, när man når ett visst värde, som kallas modul, siffrorna "vrids" till noll igen. Till exempel räknar klockan ner med modul 12: den visar 10, 11 och 12 timmar och återgår sedan till 1.
   • Många räknare har en mod -nyckel. I slutet av detta avsnitt visas hur man manuellt beräknar denna funktion för stora tal.
3. 3 Lär dig mer om fallgroparna i Fermats lilla sats. Alla nummer för vilka testvillkoren inte är uppfyllda är sammansatta, men resten av siffrorna är bara förmodligen är enkla. Om du vill undvika felaktiga resultat, sök n i listan över "Carmichael -nummer" (sammansatta nummer som uppfyller detta test) och "Fermat pseudoprime -nummer" (dessa nummer uppfyller testvillkoren endast för vissa värden a).
4. 4 Om det är lämpligt, använd Miller-Rabin-testet. Även om denna metod är ganska besvärlig för manuella beräkningar, används den ofta i datorprogram. Det ger acceptabel hastighet och färre fel än Fermats metod. Ett sammansatt tal tas inte som ett primtal om beräkningar utförs för mer än ¼ -värden a... Om du slumpmässigt väljer olika värden a och för dem alla kommer testet att ge ett positivt resultat, vi kan anta med en ganska hög grad av förtroende att n är ett primtal.
5. 5 För stora siffror, använd modulär aritmetik. Om du inte har en modkalkylator till hands, eller om räknaren inte är utformad för att hantera så stora siffror, använd kraftegenskaper och modulär aritmetik för att göra beräkningarna enklare. Nedan är ett exempel för ${ displaystyle 3 ^ {50}}$ mod 50:
   • Skriv om uttrycket i en bekvämare form: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Manuella beräkningar kan kräva ytterligare förenklingar.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Här tog vi hänsyn till egenskapen för modulär multiplikation.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Del 3 av 3: Användning av den kinesiska restsatsen

1. 1 Välj två nummer. Ett av siffrorna måste vara sammansatt, och det andra måste vara exakt det du vill testa för enkelhet.
   • Nummer 1 = 35
   • Nummer 2 = 97
2. 2 Välj två värden som är större än noll respektive mindre än siffrorna Number1 och Number2. Dessa värden får inte vara desamma.
   • Värde1 = 1
   • Värde2 = 2
3. 3 Beräkna MMI (Mathematical Multiplicative Inverse) för Number1 och Number2.
   • Beräkna MMI
     • MMI1 = Number2 ^ -1 Mod Number1
     • MMI2 = Number1 ^ -1 Mod Number2
   • Endast för primtal (detta kommer att ge ett tal för sammansatta tal, men det kommer inte att vara hans MMI):
     • MMI1 = (Number2 ^ (Number1-2))% Number1
     • MMI2 = (Number1 ^ (Number2-2))% Number2
   • Till exempel:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Skapa en tabell för varje MMI ner till log2 -moduler:
   • För MMI1
     • F (1) = Antal2% Antal1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Antal1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Antal1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Antal1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Antal1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Antal1 = 1 * 1% 35 = 1
   • Beräkna parade nummer 1 - 2
     • 35 -2 = 33 (10001) bas 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • För MMI2
     • F (1) = Antal1% Antal2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Antal2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Antal2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Antal2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Antal2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Antal2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Antal2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Antal2 = 35 * 35 mod 97 = 61
   • Beräkna det parade numret 2 - 2
     • 97 - 2 = 95 = (1011111) bas 2
     • MMI2 = (((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Beräkna (Value1 * Number2 * MMI1 + Value2 * Number1 * MMI2)% (Number1 * Number2)
   • Svar = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Svar = (2619 + 4270)% 3395
   • Svar = 99
6. 6 Kontrollera att Number1 inte är primtal
   • Beräkna (Svar - Värde1)% Antal1
   • 99 – 1 % 35 = 28
   • Eftersom 28 är större än 0 är 35 inte ett primtal.
7. 7 Kontrollera att Number2 är primtal.
   • Beräkna (Svar - Värde2)% Antal2
   • 99 – 2 % 97 = 0
   • Eftersom 0 är 0 är 97 troligen ett primtal.
8. 8 Upprepa steg 1 till 7 minst två gånger till.
   • Om du får 0 i steg 7:
     • Använd ett annat Number1 om Number1 inte är primtal.
     • Använd ett annat nummer1 om tal1 är primtal. I det här fallet bör du få 0 i steg 6 och 7.
     • Använd olika Betydelse1 och Betydelse2.
   • Om du i steg 7 konsekvent får 0, är ​​det troligt att nummer 2 är primtal.
   • Steg 1 till 7 kan resultera i ett fel om tal 1 inte är primtal och nummer 2 är en delare av nummer 1. Den beskrivna metoden fungerar i alla fall när båda talen är primtal.
   • Anledningen till att du behöver upprepa steg 1 till 7 är att i vissa fall, även om nummer 1 och nummer 2 inte är primtal, får du i steg 7 0 (för ett eller båda siffrorna). Detta händer sällan.Välj en annan Number1 (sammansatt), och om Number2 inte är primtal, kommer Number2 inte att vara lika med noll i steg 7 (förutom fallet när Number1 är en divisor för Number2 - här kommer primtal alltid att vara lika med noll i steg 7).

Tips

• Primtal från 168 till 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Även om brute force -tester är ett tråkigt test när man arbetar med stora siffror, är det ganska effektivt för små tal. Även om det gäller stora siffror, börja med att testa små delare och fortsätt sedan till mer sofistikerade metoder för att kontrollera enkelheten i siffror (om det inte finns några små delare).

Vad behöver du

• Papper, penna eller dator