Innehåll

• Att gå
• Metod 1 av 3: En första enkel uppgift
• Metod 2 av 3: Beräkning av det förväntade värdet för ett specifikt resultat
• Metod 3 av 3: Förstå konceptet
• Tips
• Förnödenheter

Förväntningsvärde är en statistisk term och ett begrepp som används för att avgöra hur användbar eller skadlig en handling kommer att vara. För att beräkna det förväntade värdet är det nödvändigt att få en god förståelse för varje utfall i en viss situation och tillhörande sannolikhet, eller sannolikheten att ett visst utfall kommer att inträffa. Stegen nedan ger några övningar som hjälper dig att förstå begreppet förväntningsvärde.

Att gå

Metod 1 av 3: En första enkel uppgift

1. Läs uttalandet. Innan du börjar tänka på alla möjliga resultat och sannolikheter är det viktigt att du förstår problemet. Till exempel ett tärningsspel som kostar € 10 per spel. En hex-form rullas en gång och dina vinster beror på antalet du kastar. Om en 6 rullas vinner du 30 €; en 5 tjänar 20 €; något annat nummer ger inget.
2. Lista alla möjliga resultat. Det hjälper till att lista alla möjliga resultat i en given situation. I exemplet ovan finns det sex möjliga resultat. Dessa är: (1) rulla en 1 och du förlorar $ 10, (2) rulla en 2 och du förlorar $ 10, (3) rulla en 3 och du förlorar $ 10, (4) rulla en 4 och du förlorar $ 10 , (5) rulla en 5 och vinn $ 10, (6) rulla en 6 och vinn $ 20.
   • Observera att varje utfall är € 10 mindre än vad som beskrivs ovan, eftersom du måste betala € 10 per spel först, oavsett resultatet.
3. Bestäm sannolikheten för varje resultat. I det här fallet är sannolikheten för 6 resultat samma. Sannolikheten för att ett slumpmässigt tal rullas är 1 på 6. För att göra det lättare att skriva ner kommer vi att skriva bråk (1/6) som ett decimal med hjälp av en miniräknare: 0,167. Skriv denna sannolikhet bredvid varje utfall, särskilt om du vill lösa ett problem med olika sannolikheter för varje utfall.
   • Din 1/6 miniräknare kan göra ungefär 0.166667. Vi avrundar detta till 0,167 för att göra det lättare att beräkna utan att offra noggrannheten.
   • Om du vill ha ett mycket exakt resultat, gör det inte till ett decimal, skriv bara 1/6 i formeln och beräkna det på din miniräknare.
4. Registrera värdet på varje resultat. Multiplicera $ av ett resultat med sannolikheten att resultatet kommer att uppstå för att beräkna hur mycket pengar det resultatet kommer att bidra till det förväntade värdet. Till exempel är resultatet av att rulla en 1 - $ 10 och sannolikheten för att rulla en 1 är 0,167. Värdet av att kasta en 1 är därför (-10) * (0,167).
   • Det finns inget behov av att beräkna dessa resultat nu om du har en miniräknare som kan utföra flera operationer samtidigt. Du får ett mer exakt resultat om du anger hela ekvationen.
5. Lägg till värdet för varje resultat för att få det förväntade värdet av en händelse. För att fortsätta med ovanstående exempel är förväntningsvärdet för tärningsspelet: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), eller - 1,67 €. Så du kan förvänta dig att förlora $ 1,67 varje gång på det här spelet (per spel).
6. Vilka är konsekvenserna av att beräkna det förväntade värdet. I exemplet ovan bestämde vi oss för att den förväntade vinsten (förlust) skulle vara - 1,67 € per kast. Detta är ett omöjligt resultat för ett spel; du kan förlora 10 €, vinna 10 € eller vinna 20 €. Men på lång sikt är det förväntade värdet en användbar, genomsnittlig sannolikhet. Om du fortsätter att spela detta spel förlorar du i genomsnitt cirka 1,67 dollar per spel. Ett annat sätt att tänka på det förväntade värdet är genom att tilldela spelet vissa kostnader (eller fördelar); du bör bara spela det här spelet om du tycker att det är värt det, njut av det nog att spendera 1,67 dollar på det varje gång.
   • Ju oftare en situation upprepas, desto mer exakt representerar det förväntade värdet det faktiska genomsnittliga resultatet. Till exempel kanske du spelar spelet 5 gånger i rad och förlorar varje gång, vilket resulterar i en genomsnittlig förlust på $ 10. Om du spelar spelet 1000 gånger till kommer det genomsnittliga resultatet dock närmare det förväntade värdet på - 1,67 € per spel. Denna princip kallas "lagen om stort antal".

Metod 2 av 3: Beräkning av det förväntade värdet för ett specifikt resultat

1. Använd den här metoden för att beräkna det genomsnittliga antalet mynt du behöver vända innan ett visst mönster inträffar. Du kan till exempel använda metoden för att ta reda på det förväntade antalet mynt att vända tills du har huvuden två gånger i rad. Det här problemet är lite svårare än ett standardproblem om förväntningsvärden, så läs ovanstående del av den här artikeln först om du inte känner till begreppet förväntningsvärde.
2. Antag att vi letar efter ett värde x. Du försöker bestämma hur många mynt du måste vända i genomsnitt för att få två huvuden i rad. Vi gör nu en jämförelse för att hitta svaret. Vi kallar svaret vi letar efter x. Vi gör den nödvändiga jämförelsen steg för steg. Vi har för närvarande följande:
   • x = ___
3. Tänk på vad som händer om den första vändningen producerar ett mynt. Detta kommer att vara fallet i hälften av fallen. Om så är fallet har du "slösat bort" en rullning, medan chansen att rulla ett huvud två gånger i rad inte har förändrats. Som med myntkastet förväntas det att du måste kasta ett genomsnittligt antal gånger innan du får ett huvud två gånger i rad. Med andra ord skulle du förvänta dig att rulla x gånger, plus de du redan har spelat. I form av en ekvation:
   • x = (0,5) (x + 1) + ___
   • Vi kommer att fylla i det tomma utrymmet när vi fortsätter att tänka på andra situationer.
   • Du kan använda bråk istället för decimaler om det är lättare eller nödvändigt.
4. Tänk på vad som händer när du kastar huvudet. Det finns 0,5 (eller 1/2) chans att du slänger en kopp första gången. Detta verkar komma närmare målet att kasta ett huvud två gånger i rad, men hur mycket? Det enklaste sättet att ta reda på är att tänka på dina alternativ på andra rullen:
   • Om det andra kastet är ett mynt är vi tillbaka till början.
   • Om andra gången också är en kopp, så är vi klara!
5. Lär dig hur man beräknar sannolikheten att två händelser kommer att inträffa. Vi vet nu att du har 50% chans att du ska kasta en kopp, men vad är chansen att du kommer att kasta en kopp två gånger i rad? För att beräkna denna sannolikhet multiplicerar du sannolikheten för båda. I det här fallet är det 0,5 x 0,5 = 0,25. Naturligtvis är detta också chansen att du kommer att rulla huvuden och sedan svansar, eftersom de båda har en chans på 0,5 att inträffa: 0,5 x 0,5 = 0,25.
6. Lägg till resultatet för "huvuden, sedan svansar" till ekvationen. Nu när vi har beräknat sannolikheten för att denna händelse inträffar kan vi gå vidare till att expandera ekvationen. Det finns en 0,25 (eller 1/4) chans att vi slösar bort att kasta två gånger utan att gå framåt. Men nu behöver vi fortfarande ett x antal fler kast i genomsnitt för att få det resultat vi vill få, plus de 2 vi redan har kastat. I form av ekvation blir detta (0,25) (x + 2), som vi nu kan lägga till ekvationen:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + ___
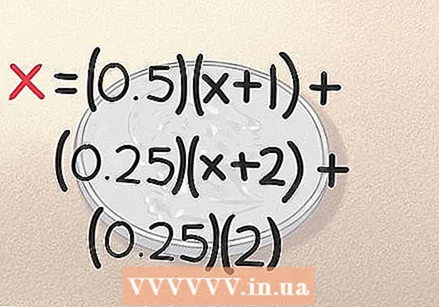7. Lägg till resultatet för "rubrik, rubrik" i ekvationen. Om du rullar huvudet, huvudet med de två första kasten av mynt, är du klar. Du fick resultatet i exakt två kast. Som vi noterade tidigare finns det en 0,25 chans att detta händer, så ekvationen för detta är (0,25) (2). Vår jämförelse är nu klar:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + (0,25) (2)
   • Om du inte är säker på att du har tänkt igenom alla möjliga situationer finns det ett enkelt sätt att kontrollera att ekvationen är komplett. Den första siffran i varje del av ekvationen representerar sannolikheten för att en händelse inträffar. Detta kommer alltid att lägga till upp till 1. Här, 0,5 + 0,25 + 0,25 = 1, så vi vet att vi har inkluderat alla situationer.
8. Förenkla ekvationen. Låt oss göra ekvationen lite enklare genom att multiplicera. Kom ihåg att om du ser något inom parentes så här: (0.5) (x + 1), multiplicerar du 0,5 med varje term som finns i den andra parentesuppsättningen. Detta ger dig följande: 0,5x + (0,5) (1) eller 0,5x + 0,5. Låt oss göra detta för varje term i ekvationen och sedan kombinera dessa termer så att det hela ser lite enklare ut:
   • x = 0,5x + (0,5) (1) + 0,25x + (0,25) (2) + (0,25) (2)
   • x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5
   • x = 0,75x + 1,5
9. Lös i x. Som i alla ekvationer måste du isolera x på ena sidan av ekvationen för att beräkna den. Kom ihåg att x betyder "det genomsnittliga antalet mynt du behöver kasta för att få huvuden två gånger i rad." När vi har beräknat x har vi också hittat vårt svar.
   • x = 0,75x + 1,5
   • x - 0,75x = 0,75x + 1,5 - 0,75x
   • 0,25x = 1,5
   • (0,25x) / (0,25) = (1,5) / (0,25)
   • x = 6
   • I genomsnitt måste du kasta ett mynt 6 gånger innan du kastar huvuden två gånger.

Metod 3 av 3: Förstå konceptet

1. Vad är ett förväntat värde egentligen. Förväntningsvärdet är inte nödvändigtvis det mest uppenbara eller logiska resultatet. Ibland kan ett förväntningsvärde till och med vara ett omöjligt värde i en given situation. Till exempel kan förväntningsvärdet vara +5 € för ett spel med ett pris på högst 10 €. Vad förväntningsvärdet indikerar är hur mycket värde en viss händelse har. Om ett spel har ett förväntat värde på + € 5 kan du spela det om du tycker att det är värt den tid och pengar du kan få per spel. Om ett annat spel har ett förväntat värde på - $ 20, så spelar du det bara om du tycker att varje spel är värt $ 20.
2. Förstå begreppet oberoende händelser. I vardagen tror många av oss att vi har en lycklig dag när några bra saker händer, och vi förväntar oss att resten av dagen ska gå den vägen.På samma sätt kan vi tro att vi har fått nog av en olycka och att något roligt verkligen måste göras nu. Matematiskt går det inte så. Om du kastar ett vanligt mynt är det exakt samma chans att du kastar ett huvud eller ett mynt. Det spelar ingen roll hur många gånger du redan har kastat; nästa gång du kastar fungerar det fortfarande på samma sätt. Myntkastet är "oberoende" av de andra kasten, det påverkas inte av det.
   • Tron att du kan ha tur eller otur när du kastar mynt (eller något annat hasardspel), eller Det faktum att all din otur nu har upphört och turen är på din sida kallas också spelare fusk (eller spelarens felaktighet). Detta har att göra med människors tendens att ta riskabla eller dumma beslut när de känner att turen är på deras sida, eller om de känner sig "lyckliga streck" eller om de känner att "turen är på väg att vända." "
3. Förstå lagen i stort antal. Du kanske tror att förväntningsvärdet inte är riktigt användbart, för det berättar bara sällan vad det faktiska resultatet av en situation är. Om du har beräknat att det förväntade värdet av ett roulette-spel är - € 1, och du spelar spelet tre gånger, kommer du vanligtvis att hamna med - € 10, eller + € 60, eller något annat resultat. "Lagen om stora siffror" hjälper till att förklara varför förväntningsvärdet är mer användbart än du kanske tror: ju mer du spelar, desto närmare förväntningsvärdet kommer det genomsnittliga resultatet att bli. När man tittar på det stora antalet händelser är det stor chans att slutresultatet ligger nära det förväntade värdet.

Tips

• För de situationer där flera resultat är möjliga kan du skapa ett kalkylblad i datorn för att beräkna det förväntade värdet med hjälp av resultaten och deras sannolikheter.
• € -beräkningarna ovan fungerar också i andra valutor.

Förnödenheter

• Penna
• Papper
• Kalkylator