Innehåll

• Steg
• Råd

Om du är matematiker eller grafisk programmerare måste du förmodligen hitta vinkeln mellan två givna vektorer. I den här artikeln visar wikiHow hur du gör just det.

Steg

Del 1 av 2: Hitta vinkeln mellan två vektorer

1. 

   Vektor definition. Skriv ner all information om de två vektorerna du har. Anta att du bara har de angivna parametrarna för deras dimensionella koordinater (även kallade komponenter). Om du redan vet längden (storleken) på en vektor kan du hoppa över några av stegen nedan.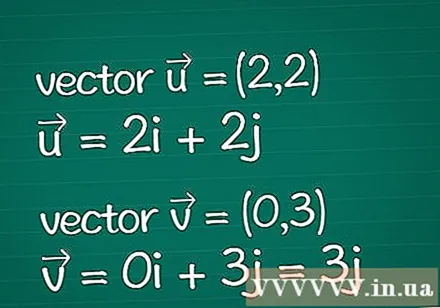
   • Exempel: Tvådimensionell vektor = (2,2) och tvådimensionell vektor = (0,3). De kan också skrivas som = 2i + 2j och = 0i + 3j = 3j.
   • Även om tvådimensionella vektorer används i exemplet i den här artikeln kan följande instruktioner gälla för vektorer med valfritt antal dimensioner.

2. 

   
   
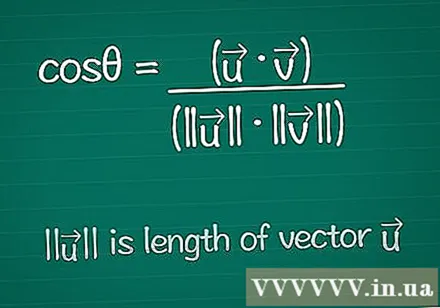
   Skriv ner cosinusformeln. För att hitta vinkeln θ mellan två vektorer börjar vi med formeln för att hitta cosinus för den vinkeln. Du kan lära dig mer om den här formeln nedan eller bara skriva ner den så här:
   • cosθ = (•) / (|||| ||||)
   • |||| betyder "längd på vektorn".
   • • är skalärprodukten för de två vektorerna - detta kommer att förklaras nedan.

3. 

   
   
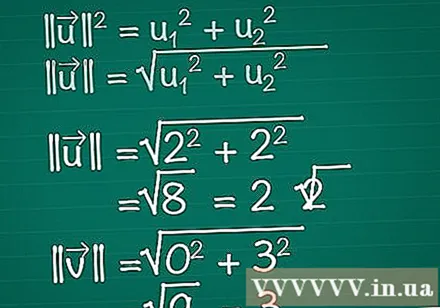
   Beräkna längden på varje vektor. Föreställ dig en rätt triangel bestående av x, y-komponenterna i vektorn och själva vektorn. Vektorn bildar triangelns hypotenus, så för att hitta dess längd använder vi Pythagoras sats. I själva verket kan denna formel enkelt utökas till en vektor med valfritt antal dimensioner.
   • || u || = u₁ + u₂. Om en vektor har mer än två element behöver du bara fortsätta lägga till + u₃ + u₄ +...
   • Följaktligen, för en tvådimensionell vektor, || u || = √ (u₁ + u₂).
   • I detta exempel, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
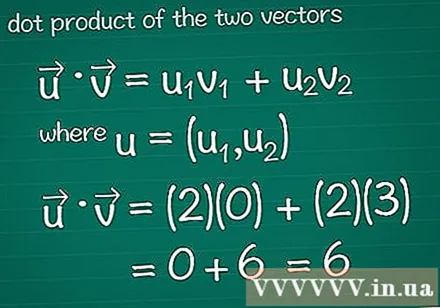
   Beräkna skalärprodukten för två vektorer. Du kanske har lärt dig metoden för vektormultiplikation, även känd som skalär detta. För att beräkna den skalära produkten i förhållande till deras sammansättning, multiplicera ingredienserna i varje riktning tillsammans och lägg sedan samman hela resultatet.
   • För grafikprogram, se Tips innan du läser vidare.
   • I matte • = u₁v₁ + u₂v₂, där, u = (u₁, u₂). Om vektorn har mer än två element, lägg bara till + u₃v₃ + u₄v₄...
   • I detta exempel är • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Detta är den skalära produkten av vektorn och vektorn.

5. 

   Sätt resultaten i formeln. Kom ihåg att cosθ = (•) / (|||| || ||). Nu vet vi både den skalära produkten och längden på varje vektor. Ange dessa i formeln för att beräkna vinkelns cosinus.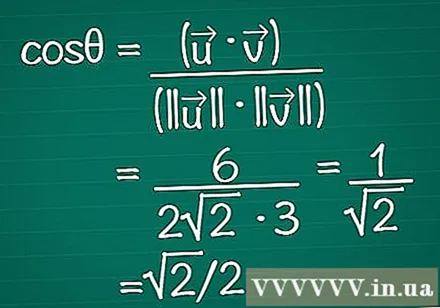
   • I vårt exempel är cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Hitta vinkeln baserat på dess cosinus. Du kan använda arccos eller cos-funktionen i en räknare för att hitta θ från ett känt cos-värde. Med vissa resultat kan du hitta vinkeln baserat på enhetscirkeln.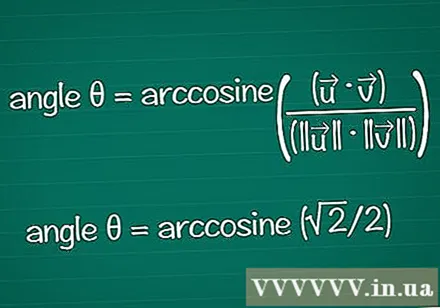
   • I exemplet är cosθ = √2 / 2. Ange "arccos (√2 ​​/ 2)" i din räknare för att hitta vinkeln. Eller så kan du hitta vinkeln θ på enhetscirkeln, vid position cosθ = √2 / 2. Det är sant för θ = /₄ eller 45º.
   • När man kombinerar allt är den slutliga formeln: vinkel θ = arkkosin ((•) / (|||| || ||))
   annons

Del 2 av 2: Bestämning av vinkelformeln

1. 

   Förstå syftet med formeln. Denna formel härrör inte från befintliga regler. Istället bildas den som definitionen av skalärprodukten och vinkeln mellan de två vektorerna. Ändå var det inte ett godtyckligt beslut. När vi går tillbaka till grundläggande geometri kan vi förstå varför denna formel ger intuitiva och användbara definitioner.
   • I exemplen nedan används tvådimensionella vektorer eftersom de är lättast att förstå och enklaste. Tredimensionella eller fler vektorer har egenskaper definierade av nästan liknande allmänna formler.

2. 

   Granska Cosines teorem. Tänk på en vanlig triangel med vinkel θ mellan sidorna a och b, motsatt sida c. Cosines sats säger att c = a + b -2abcos(θ). Detta resultat hämtas helt enkelt från grundgeometri.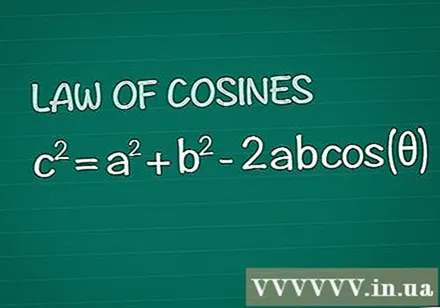

3. 

   Anslut två vektorer och bilda en triangel. Rita ett par tvådimensionella vektorer på papper, vektorer och vektorer, med θ som vinkeln mellan dem. Rita en tredje vektor mellan dessa två för att skapa en triangel. Rita med andra ord en vektor så att + =. Vektor = -.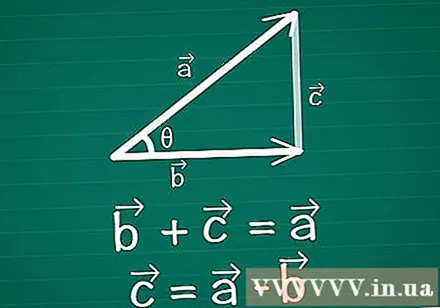

4. 

   Skriv Cosine-satsen för denna triangel. Byt ut sidolängden på vår "vektortriangel" i Cosinus teorem:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Skriv om med skalär produkt. Kom ihåg att en skalärprodukt är bilden av en vektor på den andra. Den skalära produkten av en vektor med sig själv kräver ingen projektion, för här är det ingen skillnad i riktning. Det betyder • = || a ||. Med hjälp av detta skriver vi om ekvationen:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Skriv om samma formel. Expandera vänster sida av formeln och förenkla sedan för att få formeln att använda för att hitta vinklar.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   annons

Råd

• För att ändra värden och lösa problemet snabbt, använd denna formel för valfritt par tvådimensionella vektorer: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Om du arbetar med datorgrafikprogram är chansen att du bara behöver bry dig om vektordimensionen utan att oroa dig för deras längd. Använd följande steg för att förkorta en ekvation och påskynda ditt program:
  • Normalisera varje vektor så att de är lika med 1. För att göra detta, dela var och en av vektorkomponenterna med dess längd.
  • Få den normaliserade produkten av skalären istället för den ursprungliga vektorn.
  • Eftersom längden är 1 kan vi utesluta längdelementen från ekvationen. Slutligen är den erhållna vinkelekvationen arccos (•).
• Baserat på cosinusformeln kan vi snabbt avgöra om vinkeln är spetsig eller tråkig. Börja med cosθ = (•) / (|||| ||||):
  • Vänster och höger sida av ekvationen måste ha samma tecken (positivt eller negativt).
  • Eftersom längden alltid är positiv måste cosθ ha samma tecken som den skalära produkten.
  • Därför, om produkten är en positiv, är cosθ också positiv. Vi befinner oss i enhetens första kvadrant, med θ <π / 2 eller 90º. Vinkeln att hitta är den skarpa vinkeln.
  • Om den skalära produkten är negativ är cosθ negativ. Vi befinner oss i den andra kvadranten av enhetscirkeln, med π / 2 <θ ≤ π eller 90º <θ ≤ 180º. Det är fängelseshörnet.